3강 요약
함수 F로 classifier(network) 정의 (x : input data, W : weights, 출력 : score vector)
Loss function 으로 우리의 함수 F가 얼마나 성능이 안좋은지 확인 (e.g. SVM, BCE 등...)
함수 F가 training dataset에만 fit 하는 것을 방지하기 위해(우리의 목표는 test dataset) Regularization term 추가
Loss가 가장 낮아지는 W를 찾고자 Gradient Descent 활용
Computational graphs

우리는 최종적으로 gradient 값을 자동으로 계산하기 위해 analytic gradient를 사용할 것이다.
Computational graph 를 활용하여 analytic gradient 계산 단계를 확인해보자.
위의 그래프에서 각 노드는 연산 단계를 의미한다.
Computational Graph를 사용해서 backpropagation 과정을 보면, gradient를 얻기 위해 graph 내부의 모든 변수에 대해 chain rule을 재귀적으로 사용하게 된다.
아래 예시에서 무슨 의미인지 확인해보도록 하자
Backpropagation: a simple example

위에 예시에서 x, y, z가 입력으로 들어오고 중간 노드들에서 계산이 이루어진다.
최종 결과값인 f의 output은 -12가 되는데, 이 -12가 loss에 미치는 영향(미분값)은 1이다.
이제 backpropagation에서 chain rule을 적용해가며 각 중간 단계에서의 미분값을 구할 수 있다.
중간 값의 미분값은 각 요소가 최종 loss에 얼만큼의 영향을 미치는지라고 생각해 볼 수 있다.

우리는 각 노드와 각 노드의 local 입력에 대해서만 알고 있다.
위에서 local 입력은 x, y이고 출력은 z이다.
우리는 이를 통해 local gradient를 구할 수 있다.

⭐ 다시 정리
Backpropagation 과정에서 local gradient와 upstream gradient를 곱하는 이유는 연쇄 법칙(Chain Rule) 때문이다.

연쇄 법칙에 따르면, 함수 가 있고 인 경우, 에 대한 의 미분은 다음과 같이 나타낼 수 있다.

여기서 이다.
딥러닝에서는 손실 함수를 각 층의 파라미터로 미분할 때 backpropagation은 연쇄 법칙을 사용하여 각 층의 그래디언트를 계산한다.
- "Local gradient" : 현재 층의 활성화 함수의 미분.
입력에 대한 출력의 미세한 변화에 대한 층 내의 변화를 측정 - "Upstream gradient"는 현재 층 이후의 층에서 전달된 그래디언트.
이후 다음 층에서 손실 함수의 그래디언트가 현재 층의 출력에 어떻게 영향을 미치는지를 측정.
따라서 이 두 그래디언트를 곱함으로써, 현재 층의 가중치와 편향에 대한 손실 함수의 그래디언트를 효과적으로 계산할 수 있게 되는 것이다.


add gate는 local gradient가 1이기에 같은 gradient를 받으므로 gradient distributor로
max gate는 둘 중 하나를 선택하므로 gradient router로,
mul gate는 서로의 값으로 부터 영향을 받으므로 gradient swithcer라고 생각할 수 있다.

여러 노드와 연결된 하나의 노드가 있다고 가정해보자.
이때는 upstream gradient 값들을 합해서 하나의 노드에서 받게 된다.

앞에서는 스칼라만 다뤘는데 x, y, z가 벡터라면 어떻게 해야될까?
=> 앞에서 한 것과 동일하다.
다만 gradient가 Jacobian 행렬이 된다. (각 요소의 미분을 포함하는 행렬)
ex) x의 각 원소에 대해 z에 대한 미분을 포함하는

4096차원의 벡터 입력을 받는다고 가정하자.
위의 회색 박스(노드)는 벡터의 각 요소와 0을 비교해서 최대값을 반환한다.
이렇게 되면 출력값은 4096차원의 벡터가 된다.
그렇다면 위에서 Jacobian matrix의 사이즈는 몇이 될까?
Jacobian 행렬의 각 행은 입력에 대한 출력의 편미분이 된다.
=> (4096)^2 가 된다.
Q: what is the size of the Jacobian matrix? [4096 x 4096!]
A: in practice, we process an entire minibatch (e.g. 100) of examples at one time:
i.e. Jacobian would technically be a [409,600 x 409,600] matrix :\
Q2: what does it look like?
max(0,x)에서 어떤 일이 일어나는지 생각해보자.
이때 편미분에 대해 생각해 볼 수 있다.
입력의 어떤 차원이 출력의 어떤 차원에 영향을 줄까?
Jacobian 행렬에서 어떤 종류의 구조를 볼 수 있나? --> 대각선
입력의 각 요소, 첫 번째 차원은 오직 출력의 해당 요소에만 영향을 준다.
따라서 우리의 Jacobian 행렬은 대각행렬이 될 것이다.
하지만 Jacobian 행렬을 작성하고 공식화할 필요는 없다.
우리는 출력에 대한 x의 영향에 대해서 그리고 이 값을 사용한다는 것과
우리가 계산한 gradient의 값을 채워 넣는다는 사실만 알면 된다.





- Neural networks는 보통 매우 크기에 모든 파라미터에 대한 미분값을 직접 계산하는 것은 거의 불가능하다.
- Backpropagation은 모든 입력/파라미터/중간 단계의 미분값을 계산하기 위해 computational graph에서 chain rule을 재귀적으로 적용하는 것이다.
- forward : 연산 결과를 계산하고 gradient 계산을 위해 필요한 중간 값들을 메모리에 저장한다.
- backward : 입력이 loss function에 미치는 미분값을 계산하기 위해 chain rule을 적용한다.
Neural Networks
Neural Networks


신경망은 함수들의 집합(class)으로
비선형의 복잡한 함수를 만들기 위해서 간단한 함수들을 계층적으로 여러개 쌓아올리는 형태이다.

세포체(cell body)는 들어오는 신호(input)을 종합하여 축삭(axon)을 통해 다음 세포체에 전달한다.
이는 앞에서 살펴본 computational node의 동작과 비슷하다.
뉴런은 이산 spike 종류를 사용해서 신호를 전달하는데 이는 활성화함수와 유사한 역할을 한다고 볼 수 있다.

사실 뉴런은 우리가 생각하는 것보다 훨씬 복잡하게 동작한다.
단순히 w0처럼 단일 가중치를 가지지 않고 복잡한 비선형 시스템을 갖는다.
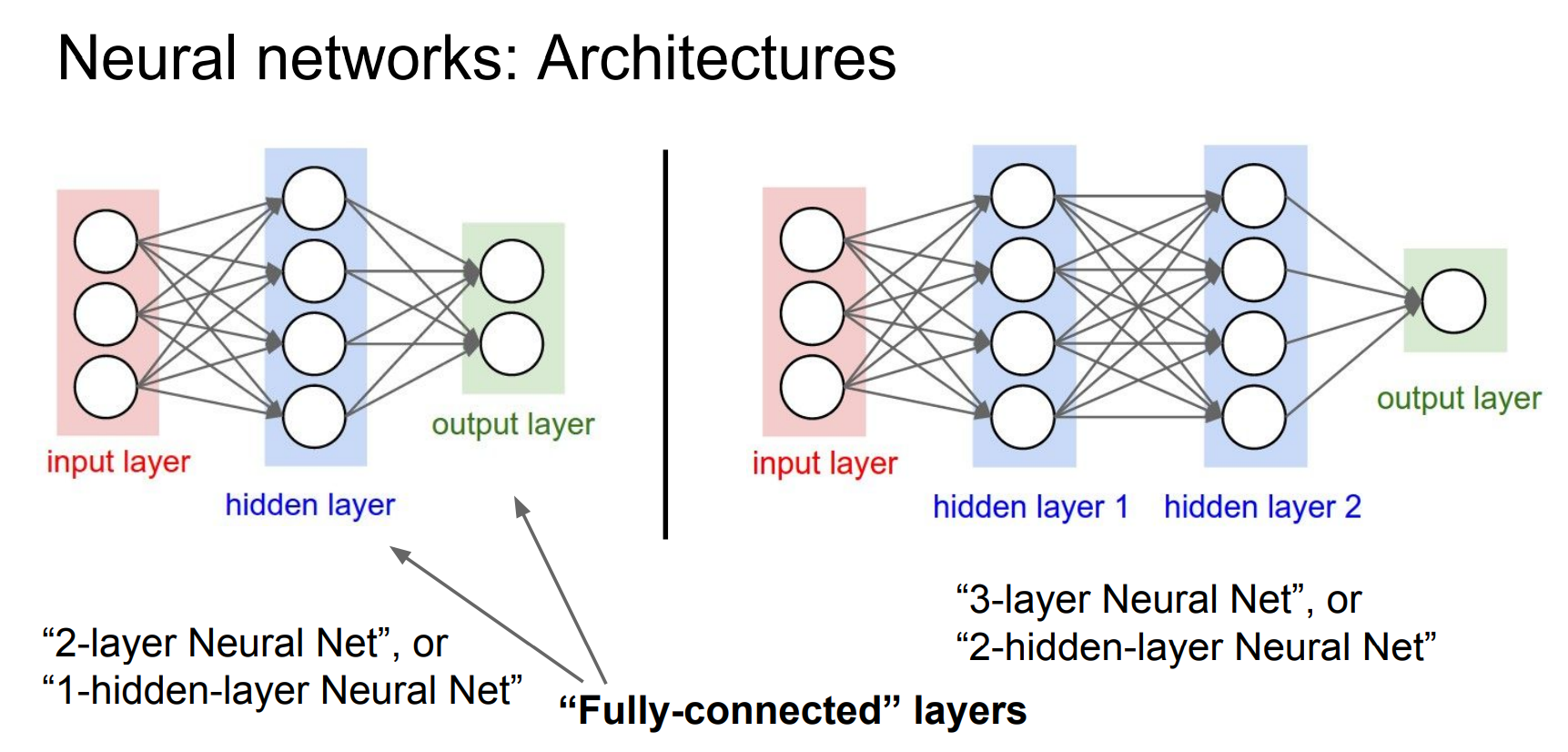
왼쪽과 같은 2레이어 신경망은 두 개의 선형 레이어를 가지고 있는 것으로
하나의 히든 레이어를 가진 네트워크라고 볼 수 있다.
Example feed-forward computation of a neural network
class Neuron :
def neuron_tick(inputs):
#assume inputs ans weights are 1-D numpy arrays and bias is a number
cell_body_sum = np.sum(inputs * self.weights) + self.bias
firing_rate = 1/0 / (1.0 + math.exp(-cell_body_sum)) #sigmoid
return firing_rate
We can efficiently evaluate an entire layer of neurons

Summary
- We arrange neurons into fully-connected layers
- The abstraction of a layer has the nice property that it allows us to use efficient vectorized code (e.g. matrix multiplies)
- Neural networks are not really neural
- Next time: Convolutional Neural Networks
'인공지능 🌌 > CS231n' 카테고리의 다른 글
| CS231n 5강 Convolutional Neural Networks (0) | 2024.03.20 |
|---|---|
| CS231n 3강 Loss Functions and Optimization (1) | 2024.03.07 |
| CS231n 2강 Image Classification Pipeline (0) | 2024.03.07 |